Testimonials
–Review from The Mathematical Olympiad Handbook, by A. Gardiner
“[A Mathematical Mosaic] is a collection of wonderful topics from number theory through combinatorics to game theory, presented in a fashion that seventh- and eighth-grade students can handle yet high school students will find challenging.”–John Cocharo, Saint Mark’s School of Texas, Dallas, TX
Free PDF Download of Chapter 4
Ravi Vakil, Professor of Mathematics at Stanford University, is one of the foremost mathematicians in the world today. In his undergraduate years, he placed among the top 5 competitors in the prestigious William Lowell Putnam Mathematical Competition, earning him the top award of “Putnam Fellow” in each year–an achievement matched by only 8 people since its inception in 1938. His stellar performance prompted the San Francisco Chronicle to describe him as “a legend in the world of math competitions.”
In this exciting book, A Mathematical Mosaic, Ravi Vakil, a preeminent winner of International Mathematics Olympiads, develops some powerful problem-solving ideas underpinning the major branches of mathematics and weaves them into a mosaic that reveals their interconnections.
The mathematics is presented at the level of the capable high school mathematics student, but there is much substance for the advanced undergraduate and the intelligent lay reader. You will find this book an invaluable source of enrichment problems and ideas.
The style is informal, friendly, and often humorous. In this book, Professor Vakil profiles ten other mathematics olympiad winners including Noam Elkies, the youngest professor to achieve tenure at Harvard, describing how their lives unfolded a decade or so after their olympiad triumphs.
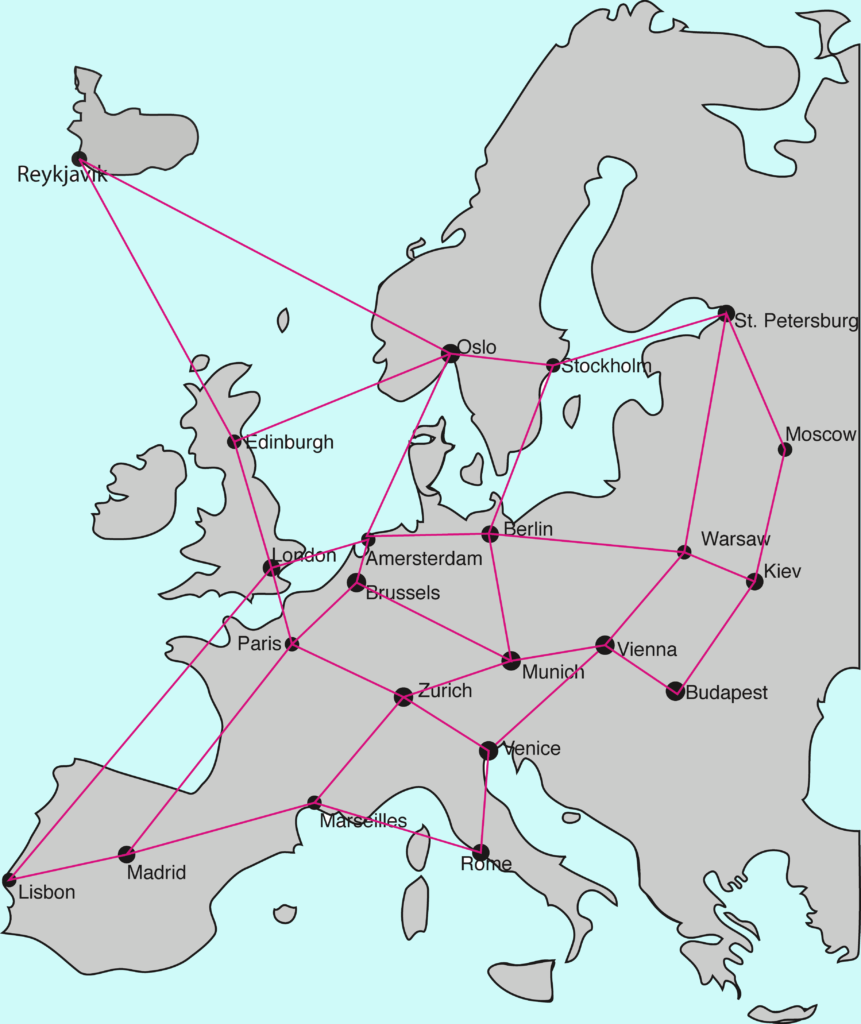
Can Sherlock catch Moriarty?
Elementary My Dear Watson!
Sherlock Holmes, master of logical deduction, chases the elusive Moriarty through Europe. One player plays the dashing and daring Holmes, and the other player plays Moriarty.
The Game
This battle of wits can be played in the airports of Europe. A less expensive alternative is to use this map. Each of the dots represents a city where the chase can take place, and the players can indicate their position by pointing at a city with a pencil or a pen. The straight lines indicate air routes where the players may travel. Sherlock begins in Stockholm, where he begins his famous chase. Moriarty starts off in Paris, where he has just stolen the Mona Lisa. Each player, in his or her turn, may jump from one city to another connected by an air link. Holmes, being true and noble, goes first. If Holmes lands in the same city as Moriarty, he captures Moriarty after an exciting car chase and wins the game. If Holmes does not catch Moriarty in fifteen or fewer moves, the villain escapes and wins the game.
