
Adrien-Marie Legendre was born on September 18, 1752, in Paris, France, into a wealthy family, and from an early age received a strong education in mathematics and science. He studied at the Collège Mazarin in Paris and later at the Collège de France, where he was influenced by the renowned mathematician and physicist Pierre-Simon Laplace. He graduated with a doctorate in mathematics and physics in 1770.
The French Revolution that began in 1789 with the storming of the Bastille continued with the mass beheading of people deemed to be members of the French aristocracy. During the Reign of Terror that was raging in 1793, Legendre’s private wealth was confiscated and he managed to survive only through the help of Marguerite-Claudine Couhin whom he had married that year. In the following year, Legendre published Éléments de géométrie, that became the standard text for the study of Euclidean geometry for more than a century.
In 1799, Napoleon became the ruler of France and in 1803, reorganized the Institut National and Legendre was appointed a member of the Geometry section. Until 1812, Legendre served as mathematics examiner for graduating artillery students at the École Militaire and until 1815 as permanent mathematics examiner for the École Polytechnique.
Legendre is well-known for his work in number theory. One of his most famous achievements was his co-discovery (with Euler) of quadratic reciprocity, although it was left to Gauss to provide a rigorous proof of that relationship. (An integer b is said to be a quadratic residue modulo p if there is an integer x such that 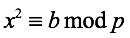
Legendre’s most significant contribution may be his three-volume treatise titled Exercices de Calcul Intégral, published in 1811, 1817 and 1819. In this work he introduced the basic properties of elliptic integrals, beta functions and gamma functions. In 1830, he gave a proof of Fermat’s Last Theorem for n = 5, i.e., there are no whole numbers x, y, z such that x5 + y5 = z5. Legendre’s work in calculus laid the groundwork for the study of elliptic curves, which are essential in modern cryptography. In his 1995 proof of Fermat’s Last Theorem (for all integers, n), Andrew Wiles used the previously established properties of elliptic curves.
Legendre also made important contributions to the field of statistics. He is generally credited with the invention of the method of least squares, although there is some evidence that Gauss may have used this process before Legendre. Most graphing calculators have built-in software that apply the method of least squares to minimize the sum of the squares of the differences between the observed and predicted values. This yields the equation of the best-fitting line or curve through a set of data points
Legendre also contributed to the development of methods for calculating the Earth’s shape and size as well as the distances between the Earth’s meridians, facilitating the development of accurate maps and navigation charts. This enabled him to contribute to the development of the metric system in which the meter was defined as one ten-millionth of the length of the meridian arc on the Earth’s surface from the equator to the north pole.
In 1824, when Legendre refused to vote for the government’s candidate for the Institut National, his pension was terminated. He and his wife were rendered penniless and soon after, Legendre suffered a long and painful illness resulting in his death on January 9, 1833.
Adrien-Marie Legendre’s work has had a lasting impact on mathematics, and his contributions to number theory, calculus, and statistics continue to be studied and utilized by mathematicians and scientists worldwide. The Legendre symbol, Legendre polynomials, and Legendre transformation are named after him in recognition of these significant mathematical achievements.
