
Corrado Gini was born on May 23, 1884 near Treviso, Italy. On graduation from high school, he enrolled in the Faculty of Law at the University of Bologna where he took a wide range of subjects, including statistics, mathematics and economics. He graduated with a law degree in 1905, but his interests continued to shift toward applying statistics to the study of economics. In 1912, Gini published a paper in which he attempted to quantify income inequality using an index subsequently named the Gini coefficient. He assigned a value of 0 to the Gini coefficient of a perfectly egalitarian society in which everyone has the same income. At the other extreme, a Gini coefficient of 1 was assigned to a society with maximal inequity in which one individual earns all the income and everyone else earns nothing. To measure the dispersion of incomes from a population of n people, he proceeded as follows:
• Sum the absolute difference in income between each pair of people in the population.
• Divide this sum by 2n times the total income to obtain a fraction between 0 and 1. That fraction, called the Gini coefficient is close to 0 when there is little income inequality and close to 1 when there is significant inequality.
In mathematical notation, the Gini coefficient is:
where xi denotes the income of the ith person.
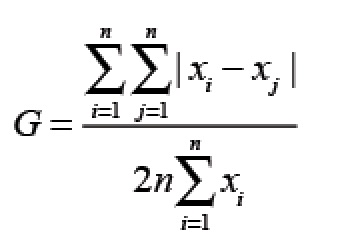
In 2015, the OECD (Organization of Economic Development) listed Gini coefficients for its member nations.Most of the nations had a Gini coefficient between 0.4 and 0.5, before taxes and transfer payments. Progressive tax policies that draw higher taxes from those with larger incomes, generally reduced these coefficients to the range between 0.3 and 0.4 after all the taxes and transfer payments were made. Among these countries, South Korea had the smallest Gini coefficient at 0.344 and Italy the highest at 0.534. The United States came in at 0.486 and Canada at 0.441, falling to 0.378 and 0.324 respectively after taxes and transfers. The highest Gini coefficients occur in the nations of Africa and South America where there is extreme poverty. At the other extreme, the Scandinavian countries such as Norway, Sweden and Denmark have Gini coefficients around 0.42 before taxes, and strong socialist policies further reduce this to about 0.25 after taxes and transfers, yielding the smallest inequities.
Although Gini developed a formula to measure wealth distribution, we may never be able to determine whether there is an ideal value for the genie coefficient.
