While it may seem that most of those with very high income have high IQ’s, the converse is not necessarily true. That is, there may be many people of very high IQ who do not have a high income. In fact, there is something strange in the relationship between IQ and income in the high-IQ group. During a dinner debate with Amy Chua (known as “Tiger Mom”) Larry Summers, President of Harvard from 2001–2006, quipped, “At Harvard, the A students tend to become professors and the C students become wealthy donors.”
Summers’ facetious comment actually carries more than a grain of truth, and it challenges the assumption that high intelligence necessarily results in high income. Among the crème de la crème in the intellectual arena are those gifted students who win medals in the mathematics olympiads and the collegiate Putnam Competition.
Many of these go on to win a Fields Medal or a Nobel Prize. But what are their career trajectories? Table 9–3 reproduced from my book on intelligence, provides a snapshot of the careers of 11 Mathematics Olympiad medal winners, between 10 and 20 years after their victories.
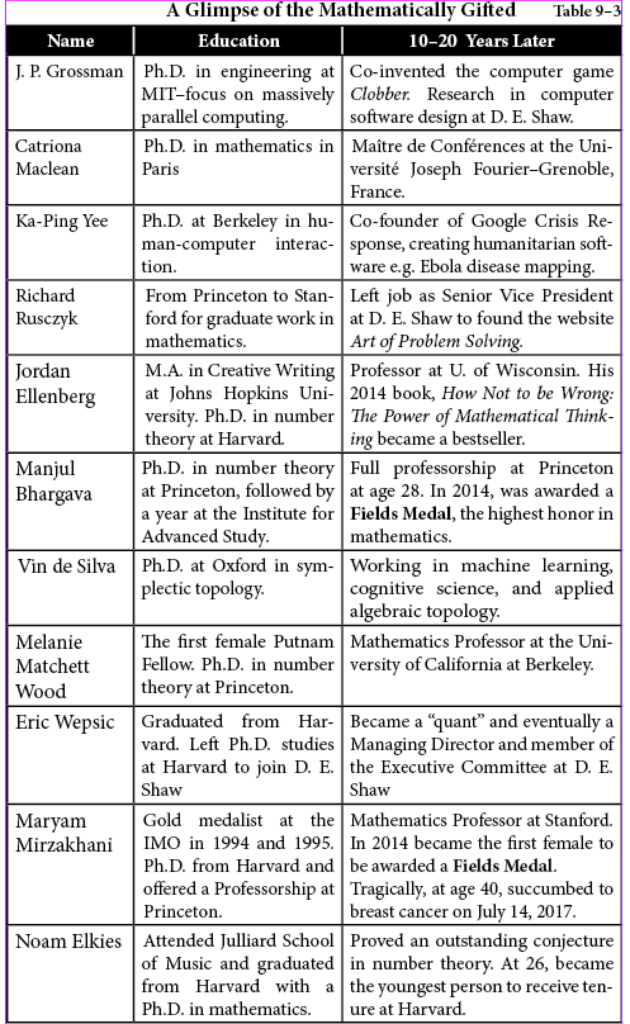
The information in Table 9–3 was compiled from A Mathematical Mosaic: Patterns & Problem Solving by Ravi Vakil, Professor of Mathematics at Stanford.
Vakil, himself an Olympiad winner par excellence, won a Silver Medal in 1986 at the International Mathematical Olympiad (IMO) in Warsaw, a Gold Medal at the IMO in Havana in 1987, and another in Canberra in 1988. As if dominating mathematics wasn’t enough, he also won first prize in the Canadian Association of Physics Competition and led his high school computer team to three Ontario championships. During his undergraduate years, he placed among the top 5 competitors in the prestigious William Lowell Putnam Mathematical Competition, earning him the top award of “Putnam Fellow” in each year. Since its inception in 1938, only 8 competitors have been able to achieve this amazing feat. His stellar performance prompted the San Francisco Chronicle to describe him as “a legend in the world of math competitions.”
We observe that, except for Richard Rusczyk, none of the uniquely talented high-IQ people displayed in Table 9-3 are entrepreneurs. Though they all have incomes that are significantly higher than average, they are not likely to become billionaires. The implicit assumption in the challenge, “If you’re so smart, why ain’t you rich?” is that everyone wants to be rich and those who aren’t have failed. On the contrary, those of high intelligence often have very different goals, aspiring to solve a famous unsolved mathematical problem, to construct a paradigm that changes how we understand our world, or to write an engaging novel. A tenured professorship at a prestigious university provides enough income for a very comfortable lifestyle, and more importantly, enables an individual to pursue an intellectual passion.
