Sometimes the intuitive sense is so compelling that we have trouble accepting truth–even in the face of absolute proof. The celebrated coincident birthday problem is an excellent example of counterintuitive problem that creates cognitive dissonance.
Coincident Birthday Problem: What is the probability that in a randomly chosen group of 24 people, there are at least 2 people with the same birthday? (i.e., born on the same day and month, but not necessarily the same year)

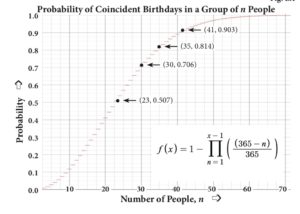
The gentleman in the picture has a better than even chance of impressing his associates with his clairvoyant power. Most people would not suspect that the probability of coincident birthdays exceeds 50% for a randomly selected group of 23 or more. They reason, “Since there are 365 or 366 days in a year, how can it be more likely than not that a randomly selected set of only 23 of them will contain two that are the same?” The result becomes even less intuitive when the group is expanded by a few more people. For example, it is almost certain that a randomly chosen group of 35 people will contain two people with the same birthday. In fact, the probability is 81.4%! The proof is given below.
This problem is best approached by calculating the probability that there is no coincidence. To this purpose, imagine that the people enter the room one at a time. To avoid coincidence, the second person must have a birthday that is different from the first person in the room, the third person must have a birthday that differs from the first two, and so on …

Therefore, the probability that there are two birthdays on the same day in a group of 35 people is 1 – 0.186 or 0.814, i.e., 81.4% The graph below shows the probability of coincident birthdays in a group of n people