In spite of our confidence in our intuition, we are often fooled by the gap between our senses and reality. This was evident in the counterintuitive birthday problem that we posted a few days ago. Another of these famous counterintuitive problems, known as the Monty Hall Dilemma, has created a lot of controversy and sometimes vitriolic discussion.
Marilyn vos Savant, is known for her widely popular column Ask Marilyn that appears in the Sunday magazine Parade. In 1988, she was entered into the Guinness Book of Records Hall of Fame as possessor of the highest measured IQ of 228. In her column, Marilyn, answers questions of a mathematical or scientific nature posed by readers. Some of the counterintuitive problems she addresses have sparked widespread controversy and stimulated discussion among amateur and professional mathematicians.
On September 9, 1990, the letter shown below appeared in the Ask Marilyn column of Parade magazine.

Dear Marilyn:
Suppose you’re on a game show, and you’re given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say number 1, and the host, who knows what’s behind the doors, opens another door, say number 3, which has a goat. He says to you, “Do you want to pick door number 2?” Is it to your advantage to switch your choice of doors?
Craig F. Whitacker, Columbia, Maryland
Note for those who’ve never seen Let’s Make a Deal:
After the contestant chooses a door, the host follows these 2 rules:
- If the car is behind the chosen door, the host chooses at random one of the two doors hiding a goat, opens it and offers the contestant the opportunity to switch from their original choice.
- If a goat is behind the chosen door, the host opens the other door hiding a goat and again offers the contestant the opportunity to switch.
Marilyn’s Answer
Dear Craig:
Yes, you should switch. The first door has a 1/3 chance of winning, but the second door has a 2/3 chance. Here’s a good way to visualize what happened: Suppose there are a million doors, and you pick door number 1. Then the host, who knows what’s behind the doors and will always avoid the one with the prize, opens them all except door number 777,777. You’d switch to that door pretty fast, wouldn’t you?
Marilyn’s answer triggered a maelstrom of emotional reaction, expressing outrage, anger and vitriol. Three of these are reprinted below.
Dear Marilyn: It is apparent from your “Ask Marilyn” column, … that being smart is no guarantee of being correct. Your analysis of the game-show probabilities, and the analogy involving the pea under a shell reveals a misunderstanding of the rudiments of probability theory, and an appalling lack of logic, …… I urge you to lower your mantle of omniscience and seek the advice of experts when the subject matter is outside your area of expertise. Your ignorant responses are hurting the fight against mathematical illiteracy.
– D. L. Professor of Mathematics
Dear Marilyn: Since you seem to enjoy coming straight to the point, I’ll do the same. In the following question and answer, you blew it! Let me explain. If one door is shown to be a loser, that information changes the probability of either remaining choice, neither of which has any reason to be more likely, to 1/2. As a professional mathematician, I’m very concerned with the general public’s lack of mathematical skills. Please help by confessing your error and in the future being more careful.
–R. S. Ph.D., George Mason University
Dear Marilyn: You made a mistake, but look at the positive side. If all those Ph.D.’s were wrong, the country would be in some very serious trouble.
–E. H. Ph.D., U.S. Army Research Institute
Was Marilyn correct in her response? Think about it before you read on.
Marilyn’s Argument
In essence, Marilyn argued that in the scenario where there are a million doors, the probability that the contestant chose the door hiding the car would be one-millionth or 0.000001. Once the host opens all but one of the remaining 999,999 doors, the probability that the car is behind one of the two unopened doors is 1. Therefore, the probability that the car is behind the door not chosen by the contestant would be 1 – 0.000001 or 0.999999.
Still Not Convinced?
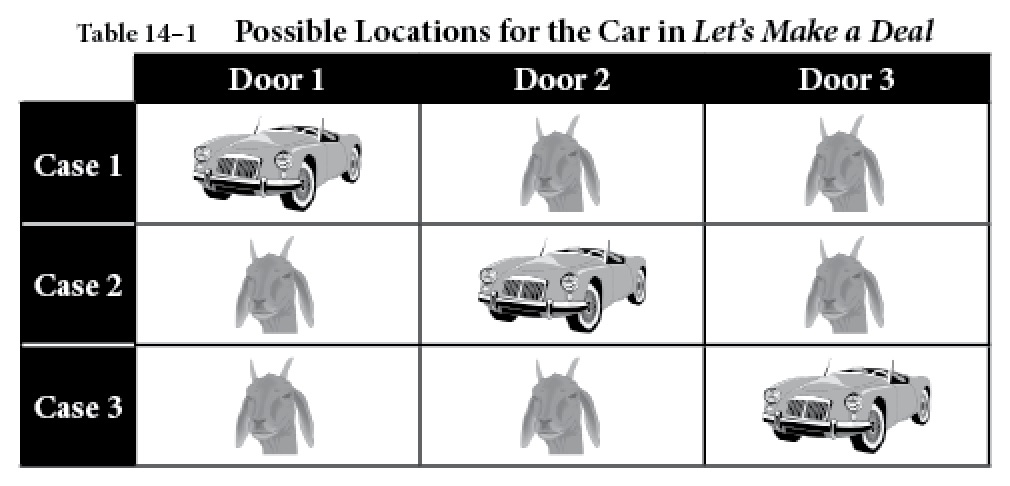
Table 14-1 (from Intelligence, IQ & Perception) below shows the three possible ways that the car can be hidden behind one of the three doors, labeled “Case 1,” “Case 2,” and “Case 3.”
Table 14–1 Possible Locations for the Car in Let’s Make a Deal
The tree diagram in figure 14.1 below, shows the probabilities of each of the four possible events that can occur when the contestant chooses Door 1.
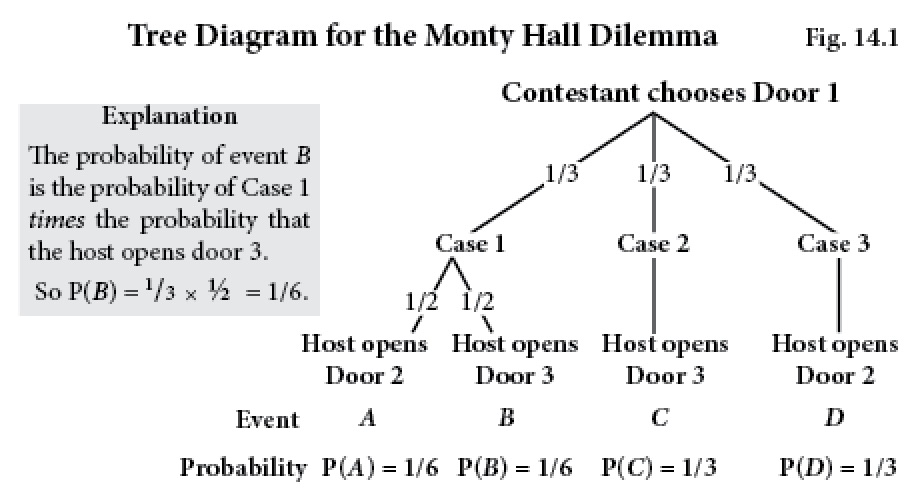
The tree diagram shows that B and C are the only events in which the host opens Door 3. But P(B) = 1/6 while P(C) = 1/3. That is, event C (Case 2) is twice as likely as event B (Case 1) to have occurred. If, as expressed in Craig’s letter, the contestant has chosen Door 1 and the host has opened Door 3, the contestant should switch to door 2. Similarly, the contestant should switch to door 3 if the host opens door 2. In both cases, switch.
This result is counterintuitive because the probability that the car is behind any particular door is 1/3 before the host opens any doors. This is called the a priori probability, meaning that it’s the probability before any new information enters the system. However, once the host opens Door 3, events A and D are eliminated, indicating that the current situation is either event B or event C. Since event C is twice as likely as event B, the contestant should switch.
Marilyn’s answer was correct. The letters reveal that, even some professional mathematicians, whose job involves scrutinizing logical arguments, are guilty of confirmation bias–our tendency to seek confirmation rather than disconfirmation of our beliefs. Since Craig Whitacker’s letter was prompted by the game show, Let’s Make a Deal, hosted by Monty Hall, this probability problem has since been known as the Monty Hall Dilemma. See also: Monty Hall Dilemma: Part 2.
