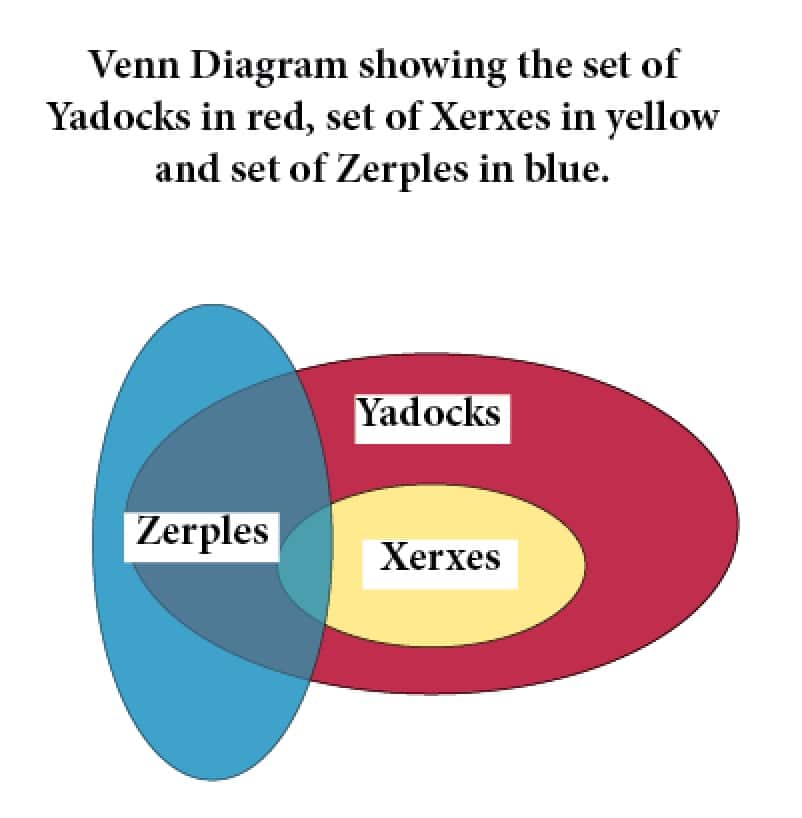
All Xerxes are also Yadocks, but only some Yadocks are Zerples.
Which of the following statements is true?
- No Xerxes can be a Zerple.
- If something is not a Yadock, it is also not a Xerxe.
- If something is a Zerple, it cannot be a Xerxe.
Answer: We can represent the statements in a Venn diagram. The statement that all Xerxes are Yadocks means that the set of Xerxes is contained in the set of Yadocks. The statement that only some Yadocks are Zerples means that the set of Yadocks and Zerples intersect but neither is a subset of the other.
When we look at the Venn diagram below, we see that statements 1 and 3 are false and statement 2 is true. That is, since every Xerxe must also be a Yadock, if it is not a Yadock, it cannot be a Xerxe.